RSA 암복호화 증명시 필요한 공식.
2011. 7. 16. 23:39 in 관련자료

336x280(권장), 300x250(권장), 250x250, 200x200 크기의 광고 코드만 넣을 수 있습니다.
1. http://en.wikipedia.org/wiki/Modular_multiplicative_inverse
2. http://en.wikipedia.org/wiki/Euler%27s_theorem
3. http://en.wikipedia.org/wiki/Totient
우선 비밀키 e 는 phi(n)과 서로소 이므로 공통 분모는 1 이다.
공개키 e를 통해서 인버스를 구한 d 역시 phi(n)과는 서로소 이며 공통 분모는 1
de = 1 (mod phi(n) )
즉 이말은 d와 e의 곱을 phi(n)으로 나눌 경우 나머지는 1.
- totien 의 함수 에서 phi(n) 을 구한다 where n 은 p 와 q 의 곱. ( 3 번 공식 활용 )
- phi(n)을 토대로 n과 서로소인 공개키 e를 구한다(서로소) (참고로 totien의 함수는 phi(n)에서 n과 서로소의 갯수를 나타낸다 , 고로 공개키 e는 1 < e < phi(n) 작은것을 pick up 하는 것) (3 번 공식 활용 )
- 여기서 구해진 e 를 토대로 phi(n)으로 나눌 경우 1이 되는 인버스를 구한다. (1 번 공식 활용 )
이제 암호화된 문장이 복호화 되는 방식에 관한 증명.
마지막 정리는 m 이 n 에 서로수 이므로 율러의 이론을 바로 따르게 됩니다.
감사 합니다.
2. http://en.wikipedia.org/wiki/Euler%27s_theorem
3. http://en.wikipedia.org/wiki/Totient
우선 비밀키 e 는 phi(n)과 서로소 이므로 공통 분모는 1 이다.
공개키 e를 통해서 인버스를 구한 d 역시 phi(n)과는 서로소 이며 공통 분모는 1
de = 1 (mod phi(n) )
즉 이말은 d와 e의 곱을 phi(n)으로 나눌 경우 나머지는 1.
- totien 의 함수 에서 phi(n) 을 구한다 where n 은 p 와 q 의 곱. ( 3 번 공식 활용 )
- phi(n)을 토대로 n과 서로소인 공개키 e를 구한다(서로소) (참고로 totien의 함수는 phi(n)에서 n과 서로소의 갯수를 나타낸다 , 고로 공개키 e는 1 < e < phi(n) 작은것을 pick up 하는 것) (3 번 공식 활용 )
- 여기서 구해진 e 를 토대로 phi(n)으로 나눌 경우 1이 되는 인버스를 구한다. (1 번 공식 활용 )
이제 암호화된 문장이 복호화 되는 방식에 관한 증명.
Concise proof using Euler's Theorem ( 2 번 공식 활용 )
To show that a message encrypted with e can be decrypted with d we need to prove
( e 로 암호화된 메시지를 d로 복호화 시킴을 보여주기 위해서는, 아래 공식을 증명할 필요가 있다 )
i.e.
Now, since 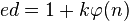 ,
,
1 번 공식에 의해서 구해진 d는 e의 인버스 관계 이므로
e * d = 1 mod phi(n)
= > e * d - 1 = k * phi(n) = > ed =1 + k * phi(n) 가 성립 됩니다.

다시 message m ^ ed 은
= m ^ ( 1 + k * phi(n) )
= m * (m ^ phi(n) ) ^ k
위의 공식에 mod n 을 할경우
( m ^ phi(n) ) mod n = 1 ( 2번 율러의 이론 활용 ) 이 되므로,
= m * (1) ^ k
= m (mod n ) where n is product of two primes.
= m
마지막 정리는 m 이 n 에 서로수 이므로 율러의 이론을 바로 따르게 됩니다.
감사 합니다.
'관련자료' 카테고리의 다른 글
| Dynamic_Designer 추가 기능 12_31 (0) | 2011.12.31 |
|---|---|
| 리눅스에서 닷넷 어플리케이션 만들기. (0) | 2011.11.28 |
| Software의 크기 및 산출관련 글 (0) | 2010.09.27 |
| Dynamic Function Loader. (0) | 2010.09.26 |
| 압축 알고리즘에서 사용된 reserved 된 값과 얻는 핵심 알고 리즘 입니다. (0) | 2010.08.04 |



 Rss Feed
Rss Feed